R-2024-076
2024年の財政検証を経て、年金制度改革に関する厚生労働省の準備は大詰めを迎えている。このような状況のなか、テレビや新聞等では、「106万円の壁」撤廃や基礎年金の給付水準の改善などに関する報道も増えてきたが、それらの議論をする以前の問題として、有識者の一部が正しいとは思えない発言やコメントをするケースも目にするようになってきた。なかでも懸念すべきものは、積立方式の有効性に対する誤解で、例えば、以下のような発言やコメントだ。
|
人口減少で労働力が減少すれば、財・サービスを生産する能力も低下するので、マネーを積み立てても意味がない。 |
筆者はこのコメントを某大学の経済学者が平然と行い流布していることに、正直、驚愕した(厚生労働省のホームページにも似た記載があるが…)。東京大学名誉教授の吉川洋氏がRIETIの論文「少子高齢化と経済成長」でも指摘するように、日本やフランス等の先進国では、「過去100年実質GDPは人口の増加率をはるかに上回る成長をしてきた」という事実を無視しているためである。実質GDPは、一定期間で生産されたすべての財・サービス(最終生産物)から物価の影響を調整したもので、いわば実物の「生産量」を示す指標である。財・サービスの生産量は、人口や労働力のみでなく、資本や全要素生産性にも依存するはずで、財・サービスの生産能力は、これらの複合要因にほかならない。その際、吉川洋氏の論文をはじめ、主流派の経済学者は、過去データの実証分析から、実質GDP成長率に対する寄与度では、労働力の影響よりも、資本や全要素生産性の影響が大きかったことを確認しているはずだ。オランダ・フローニンゲン大学のAngus Maddison教授は、経済史が専門で人口やGDP等に関する歴史的統計資料を収集している。このデータから、日本やフランス・アメリカ等の人口や実質GDPが、1901年と比較して何倍になったか計算すると、人口は1.5倍~4倍程度に過ぎないが、実質GDPは何十倍にも増加していることが分かる。つまり、人口変動が実質GDPに及ぼす影響はゼロではないが、主な要因ではない。
もっとも、財・サービスの生産能力を示す指標は、人口増加の時代と人口減少の時代では異なるかもしれない。「実質GDP=人口×一人当たり実質GDP」であり、一国で生産された財・サービスのうち、一人当たりの平均でみた消費量は「一人当たり実質GDP」で評価することも可能である。このため、人口減少の時代の財・サービスの生産能力は、実質GDPでなく、一人当たり実質GDPで評価するのが妥当かもしれない。経済学者が各国の経済成長を議論するときは、この「一人当たり実質GDP」で比較することも多い。この関係では、人口減少に突入した現在の日本でも、一人当たり実質GDP成長率は、コロナ危機などの影響で、一時的にマイナスの値に低下することがあっても、数年で均してみればプラスの値で成長している。また、冒頭のコメントが正しいとするなら、公的年金制度の持続可能性が危ぶまれるなか、老後の資産形成を促進するため、政府がNISAやiDeCoの拡充を推進しているという動きは、「マネーを積み立てても意味がない」という発言やコメントと矛盾することに気が付かないのだろうか。
以上のほか、年金制度において、例えば以下のような発言やコメントも疑問を感じる。
|
この制度改正では、基本的にデメリットは無く、メリットの方が多い。 |
この発言やコメントも、年金制度に内在する基本的な性質に矛盾している。というのも、「年金制度による所得移転政策は基本的にゼロ・サム・ゲーム的な性質をもち、誰か(例:ある世代)が得をすれば、他の誰か(例:別の世代)が損をするという性質をもつ」からである。この性質は理論的に必ず成立するにもかかわらず、制度改正の議論でも、この性質を無視した発言が時々存在する。間違った認識や情報の下で議論すると、誤った政策判断をしてしまう可能性が高まる。
やや専門的な議論になるが、世代間のケースで、年金制度に内在するゼロ・サム・ゲーム的な性質を確認しておこう。現在の年金制度は、賦課方式年金に一部の積立金を保有する「修正賦課方式」と呼ばれる仕組みである。各世代が現役期と引退期の2期間生存し、現役期に年金保険料(租税等の負担を含む)を支払い、引退期に年金を受け取るものとする。また、世代tの人口をNt、t期において現役世代が稼ぐ賃金をWt、引退世代が受け取る年金をPt-1、現役世代が支払う保険料率を![]() 、t期の積立金を
、t期の積立金を![]() とする。議論を簡略化するため、各期の金利rを一定とすると、t期における年金の予算制約式(保険料収入総額+(t-1)期の積立金=給付総額+t期の積立金)は以下となる。
とする。議論を簡略化するため、各期の金利rを一定とすると、t期における年金の予算制約式(保険料収入総額+(t-1)期の積立金=給付総額+t期の積立金)は以下となる。
![]()
この式に(t+1)期の予算制約式を代入し、似た操作を繰り返すと、初期の積立金や最終的な積立金がゼロのとき、第期以降における年金の通時的な予算制約式として以下が得られる。
![]()
年金の所得代替率を![]() とし、純負担率を
とし、純負担率を![]() とすると、
とすると、![]() であるから、上式は以下のように記載できる。
であるから、上式は以下のように記載できる。
![]()
この式の意味は極めて重要である。(1)式の左辺(NoPo)は、年金制度を導入したとき(第1期)、保険料負担をせずに年金を受給した引退世代(世代0)の人口(No)にその世代が受け取った年金額(Po)を掛けたものになっている。すなわち、年金制度という世代間所得移転政策で、世代0が受け取った年金給付総額を意味する。
他方、(1)式の右辺は、それ以降の世代の人口(Nt)に各世代の純負担![]() を掛けて現在価値に変換した上で、それらを合計したものになっている。純負担率
を掛けて現在価値に変換した上で、それらを合計したものになっている。純負担率![]() は、現役期に1単位の保険料を支払ったとき、引退期に得られる年金が
は、現役期に1単位の保険料を支払ったとき、引退期に得られる年金が![]() であり、それを現在価値に変換した上で、その収益率を示すものになっている。この純負担率θtが正の値であれば、年金制度による受益と負担との比較で、世代tは超過受益であり、純負担率θtが負の値であれば超過負担となる。
であり、それを現在価値に変換した上で、その収益率を示すものになっている。この純負担率θtが正の値であれば、年金制度による受益と負担との比較で、世代tは超過受益であり、純負担率θtが負の値であれば超過負担となる。
一般的に、この純負担率θtの値は世代で異なるが、(1)式から、純負担率が一定の値(θ)であるとき、以下の式を得ることができる。
![]()
この式の右辺の分子(NoPo)は「保険料負担をせずに世代0が受け取った年金給付総額」、右辺の分母は「各世代の賃金総額の現在価値」を表し、その比率が純負担率の平均となっている。分母は、各世代の人口成長率のほか、賃金成長率や金利が予測できれば計算できる。また、(2)式の右辺は必ず正の値であるから、平均的にみて、(1)式における世代0以降の世代の純負担率θtは必ず正の値となることを意味する。
このような視点で(1)式をみると、(1)式は「年金制度という世代間所得移転政策は、基本的にゼロ・サム・ゲーム的な性質をもち、制度導入時の引退世代が得をした分については、その分を含め、後の世代が必ず負担しないといけない」という性質を表すことが分かる。この制度導入時に得した分を「暗黙の債務」といい、純負担率θtを「暗黙の租税」という。
なお、積立方式が目指すのは「世代間の負担平準化」である。積立方式にも「事前積立方式」や「完全積立方式」などの種類があり、前者は、修正賦課方式でマクロ経済スライドの調整期間が終了した状況とも一致する。このことは、(1)式や(2)式の応用として、以下の順番で確認できる。
まず、年金制度を導入したときの引退世代は世代0であったが、マクロ経済スライドの影響を受け、所得代替率が徐々に低下して変動する世代を世代1、マクロ経済スライドが終了し、所得代替率が一定値(![]() )となる世代を世代2以降としよう。現行の年金制度では、2004年の改革で、保険料率は一定になっているので、世代2以降の保険料率は一定値(
)となる世代を世代2以降としよう。現行の年金制度では、2004年の改革で、保険料率は一定になっているので、世代2以降の保険料率は一定値(![]() )とする。このとき、世代1の純負担率を率
)とする。このとき、世代1の純負担率を率![]() とすると、(1)式は以下となる。
とすると、(1)式は以下となる。
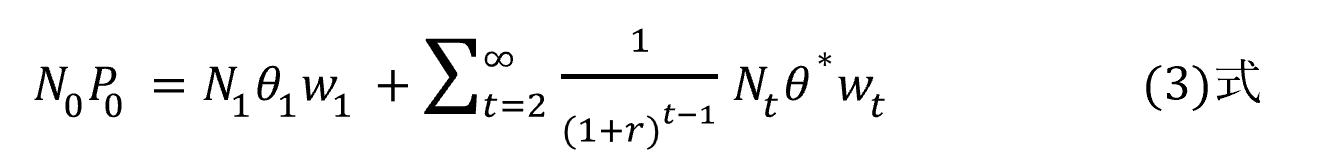
ここで、![]() は世代2以降の純負担率(
は世代2以降の純負担率(![]() )を表し、この値は一定値である。
)を表し、この値は一定値である。
他方、事前積立方式とは、年金の給付水準を削減しない限り、少子高齢化の進展で将来の保険料率を引き上げないといけなくなる事態に備えて、積立金を活用しながら、将来の給付分をあらかじめ余分に積立をしておく方式をいう。
事前積立方式も、積立金を活用しながら、世代間の負担平準化を図るが、基本的には修正賦課方式(=賦課方式+積立金)の年金制度である。このため、事前積立方式の下でも、(1)式は必ず成立する。いま、事前積立方式で、世代0や世代1の純負担率は変更せず、世代2以降の純負担率を平準化したとしよう。このときの純負担率をとすると、以下が成立する。
![]()
上式と(3)式の左辺や右辺の第1項は同じであるから、![]() が成立する。すなわち、修正賦課方式でマクロ経済スライドの調整期間が終了した状況は、事前積立方式を活用し、世代間の負担平準化を行った状況と同じなのである。にもかかわらず、冒頭の発言やコメントをする有識者が「マクロ経済スライドの重要性は評価する一方、積立方式は意味が無い」と発言することは矛盾しており、この矛盾に気が付かないのは、残念で仕方ない。
が成立する。すなわち、修正賦課方式でマクロ経済スライドの調整期間が終了した状況は、事前積立方式を活用し、世代間の負担平準化を行った状況と同じなのである。にもかかわらず、冒頭の発言やコメントをする有識者が「マクロ経済スライドの重要性は評価する一方、積立方式は意味が無い」と発言することは矛盾しており、この矛盾に気が付かないのは、残念で仕方ない。
2000年代以降、暫くの間、世代間格差の問題が政治的な問題に浮上することは少なかったが、子育てを担う現役世代の負担増も高まっており、「異次元の少子化対策」(こども未来戦略)の支援金制度の創設に関する議論で、風向きがいっきに変わったのではないか。支援金制度の創設が政治的な問題に浮上した背景には、社会保険料の負担増などが生み出す、世代間格差の問題がある。事前積立方式は、年金制度において、その世代間格差を平準化する方法の一つだ。年金制度改革の方向性を含め、正しい情報の下で国民が的確な議論をする環境整備を醸成するためには、戦略的に発信され、氾濫する情報の精査が必要である。何らかの意図をもって情報を攪乱し、一時的に問題を覆い隠しても、いつか必ず問題が顕在化するのではないか。